算法简介：

广度优先搜索（也称宽度优先搜索，缩写BFS）是树的一种遍历策略。因为它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域，故得名。

一般可以用它做什么呢？一个最直观经典的例子就是走迷宫，我们从起点开始，找出到终点的最短路程，很多最短路径算法就是基于广度优先的思想成立的。(Spfa

时间复杂度

最差情形下，BFS必须寻找所有到可能节点的所有路径，因此其时间复杂度为 O(|V| + |E|)，其中 |V| 是节点的数目，而 |E| 是图中边的数目。

空间复杂度

因为所有节点都必须被储存，因此BFS的空间复杂度为 O(|V| + |E|)，其中 |V| 是节点的数目，而 |E| 是图中边的数目。

基本实现思想：

设图G的初态是所有顶点均未访问，在G 中任选一顶点i作为初始点，则广度优先搜索的基本思想是：

（1）从图中的某个顶点V出发，访问之；并将其访问标志置为已被访问,即book[i]=true；

（2）依次访问顶点V的各个未被访问过的邻接点，将V的全部邻接点都访问到；

（3）分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，并使“先被访问的顶 点的邻接点”先于“后被访问的顶点的邻接点”被访问，直到图中所有已被访问过的顶 点的邻接点都被访问到。

依此类推，直到图中所有顶点都被访问完为止 

广度优先搜索在搜索访问一层时，需要记住已被访问的顶点，以便在访问下层顶点时，从已被访问的顶点出发搜索访问其邻接点。所以在广度优先搜索中需要设置一个队列Queue，使已被访问的顶点顺序由队尾进入队列。在搜索访问下层顶点时，先从队首取出一个已被访问的上层顶点，再从该顶点出发搜索访问它的各个邻接点。

伪代码：

void BFS()
{
    把起始源点的状态设置为已访问
    将源点加入队列； 
    while(队列元素不为空)
    {
        取出队首的元素
        for(枚举)
        {
            if(当前点能被取出的元素遍历到)
            {
                标记当前点状态为已访问;
                将当前枚举的点加入队列; 
            } 
        } 
    }
}

图解：

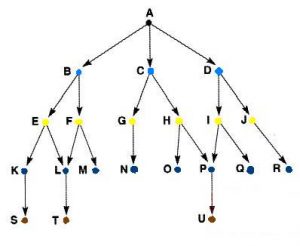
如图所示：BFS的遍历顺序分别为：

A；

B，C，D；

E，F，G，H，I，J；

K，L，M，N，O，P，Q，R；

S，T，U；

也就是说：这种图的遍历的方式是一层层向下遍历的；只有在上一层全部更新完成后才会进行下一层；

例题：

1)：给出一个地图，起点为B，终点为C，'.'代表路，'*'代表障碍，问从起点走到终点的最小步数与路径；

样例地图：

5 6
B...*.
..*...
.**.*.
..***.
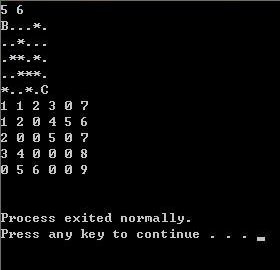
*..*.C

BFS运行结果:

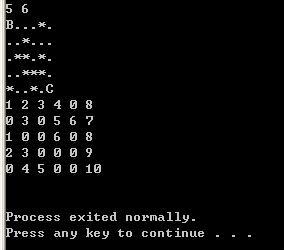
DFS运行结果：

BFS源代码：

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
char s[200];
int f[200][200];
int tmp[200][200];
int dx[5]={0,0,1,-1,0};
int dy[5]={0,1,0,0,-1};
int n,m;
int l1,l2,r1,r2;
struct map
{
    int x,y,sum;
}a[200];
void BFS()
{
    queue<map>q;
    tmp[l1][r1]=1;
    map nmp;
    nmp.x=l1;nmp.y=r1;nmp.sum=0;
    q.push(nmp);
    while(q.size())
    {
        nmp=q.front();
        q.pop();
        for(int i=1;i<=4;i++)
        {
            int dxx=nmp.x+dx[i];
            int dyy=nmp.y+dy[i];
            if(dxx>=1&&dxx<=n&&dyy>=1&&dyy<=m)
            {
                if(f[dxx][dyy]==0&&tmp[dxx][dyy]==0)
                {
                    if(dxx==l2&&dyy==r2)
                    {
                        tmp[dxx][dyy]=nmp.sum+1;
                        return ;
                    }
                    tmp[dxx][dyy]=nmp.sum+1;
                    map temp;
                    temp.x=dxx,temp.y=dyy;
                    temp.sum=nmp.sum+1;
                    q.push(temp);                   
                }
            }
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",&s[0]);
        for(int j=0;j<m;j++)
        {
            if(s[j]=='*') f[i][j+1]=1;
            if(s[j]=='B') l1=i,r1=j+1;
            if(s[j]=='C') l2=i,r2=j+1;
        }
    }
    BFS();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            printf("%d ",tmp[i][j]);
        }
        printf("\n");
    }    
}

DFS源代码;

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int f[200][200];
bool tmp[200][200];
int nmp[200][200];
char s[200];
int dx[5]={0,0,1,-1,0};
int dy[5]={0,1,0,0,-1};
int n,m;
int ans=0x7f7f7f7f;
int l1,l2,r1,r2;
int k;
void dfs(int x,int y,int sum)
{
    if(x==l2&&y==r2)
    {
        ans=min(sum,ans);
        return ;
    }
    for(int i=1;i<=4;i++)
    {
        int dxx=x+dx[i];
        int dyy=y+dy[i];
        if(dxx>=1&&dxx<=n&&dyy>=1&&dyy<=m)
        {
            if(f[dxx][dyy]==0&&tmp[dxx][dyy]==0)
            {
                nmp[dxx][dyy]=sum;
                tmp[dxx][dyy]=1;
                dfs(dxx,dyy,sum+1);
                tmp[dxx][dyy]=0;
            }
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",&s[0]);
        for(int j=0;j<m;j++)
        {
            if(s[j]=='*') f[i][j+1]=1;
            if(s[j]=='B') l1=i,r1=j+1;
            if(s[j]=='C') l2=i,r2=j+1;
        }
    }
    dfs(l1,r1,0);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            printf("%d ",nmp[i][j]);
        }
        printf("\n");
    }   
}

现在大家应该能看出DFS与BFS的区别了吧；

注意！！因为DFS会超时，甚至爆栈，所以地图寻找路径的题型必须用BFS！

2):3032: USACO 2016 Jan Bronze 2.Angry Cows

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
int n,ans;
bool book[200];
struct your
{
    int c,sum;
}a[200];
int search(int x)
{
    int k=1;
    queue<your>q;
    your tmp;
    tmp.c=a[x].c;
    tmp.sum=1;
    q.push(tmp);//将源点压入队列 
    while(q.size())
    {
        tmp=q.front();
        q.pop();
        for(int i=1;i<=n;i++)
        {
            if(book[i]==0&&abs(tmp.c-a[i].c)<=tmp.sum)//判断是否能被引爆 
            {
                k++;
                book[i]=true;
                your temp;
                temp.c=a[i].c;
                temp.sum=tmp.sum+1;
                q.push(temp);//加入队列中 
            }   
        }
    }
    return k;
}
void init()
{
    memset(book,false,sizeof book);
    for(int i=1;i<=n;i++)
        a[i].sum=0;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
        scanf("%d",&a[i].c);
    for(int i=1;i<=n;i++)
    {
        init();//清空 ，初始 
        book[i]=true;
        ans=max(ans,search(i));
    }
    printf("%d",ans);
    return 0;
}

未完待续......