(Ciel)国庆期间集训第一天啊,好激动,不过真的没想到上来就考试啊…
今天进行了NOIP第一次模拟比赛,即algorithm101……
对于algorithm101里的3道题,个人认为前两道题还是很简单的,至于第三题,DFS一直没学好,所以只是拿了20;
友情链接
【题解】国庆节集训Algorithm101 By Tonyzhao(强)
测试概况
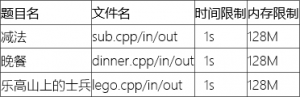
话不多说,开始分析题目:
T1 减法
考查知识点 :高精度A-B(弱化版)即A>=B>=0;
题目大意:计算A-B的值,其中 1<=A<=10^1000, 0<=B<=A。
因为是弱化版,所以还是很好写的;
直接模拟进位即可;
int lenz=0;
for(int i=1;i<=lenx;i++)
{
if(x[i]<y[i])
{
x[i]=x[i]+10;
//不用考虑x[i+1]-1<0的情况;
//因为若x[i+1]-1<0,y[i+1]一定>x[i+1]还需要进位;
x[i+1]--;
}
z[i]=x[i]-y[i];
lenz++;
}然而忽略了A-B=0的情况,丢了10分;
对于处理这种问题,我很是欣赏zty的方法:
为了防止前缀零的出现,使用ans[0]来记录高精度整数ans的长度,从前往后第一个不是0的数即为最高位。并且可解决差为零的情况—zty
void calc()
{
for(int i=1;i<=a[0];++i)
{
if(a[i]>=b[i]) ans[i]=a[i]-b[i];
else
{
--a[i+1];
a[i]+=10;
ans[i]=a[i]-b[i];
}
if(ans[i]!=0) ans[0]=i;
}
}
if(ans[0]==0) ans[0]=1; for(int i=ans[0];i>0;--i) printf("%d",ans[i]);......
对于高精度A+B和(以后也许会写的)A-B(加强版),讨论 和(差)为0的情况还是很有必要的;
而于高精度A*B(无论B为高精度和低精度)来说,必不可少的是乘积为0的情况和F[1]=1;(其实这个能调出来)
什么??高精度A/B? 我也不会写!!
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
char a[10010];
char b[10010];
int x[10010];
int y[10010];
int z[10010];
int tmp;
int main()
{
//freopen("sub.in","r",stdin);
//freopen("sub.out","w",stdout);
scanf("%s",&a[0]);
scanf("%s",&b[0]);
int lenx=strlen(a);
int leny=strlen(b);
for(int i=1;i<=lenx;i++)
{
x[i]=a[lenx-i]-'0';
}
for(int i=1;i<=leny;i++)
{
y[i]=b[leny-i]-'0';
}
int lenz=0;
for(int i=1;i<=lenx;i++)
{
if(x[i]<y[i])
{
x[i]=x[i]+10;
//不用考虑x[i+1]-1<0的情况;
//因为若x[i+1]-1<0,y[i+1]一定>x[i+1]还需要进位;
x[i+1]--;
}
z[i]=x[i]-y[i];
lenz++;
}
for(int i=lenz;i>=1;i--)
{
if(z[i]!=0)
{
for(int j=i;j>=1;j--)
{
printf("%d",z[j]);
}
tmp=1; break;
}
}
if(tmp==0) printf("0");
}T2 晚餐
考查知识点:DP
题目大意:
对于i项任务,有两种方法来解决,方法A需要A[i]个时间,方法B需要B[i]个时间,而从A切换到B(或从B切换到A)需要C[i]个时间,问完成所有任务最少花费时间;
(其实任务是吃饭,方法A是用勺子,方法B是用筷子…….)
这道题很像Vijos上的 ”更换轮胎”所以我就把这道题的思路拿过来用了,毕竟都是一类题嘛
思路如下:
定义:f[i][1]为第i盘用勺子吃时的最短时间
f[i][2]为第i盘用筷子吃时的最短时间
初始化:f[1][1]=a[1][1]+c[1];
f[1][2]=a[1][2];
f[i][1]=min(f[i-1][1],f[i-1][2]+c[i])+a[i];
f[i][2]=min(f[i-1][2],f[i-1][1]+c[i])+b[i];
答案即为min(F[n][1],F[n][2])
一开始,我是在最后的比较上加的c[1],
然而后来认为还不如在开始加上了,就改了,结果忘了把比较时加上的c[1]删了!!
导致此题全WA!!!
改正倒是很简单
我发现这处错误并改正后,就AC了
附(改后)AC代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int a[10100][4];
int c[10100];
int f[10100][4];
int main()
{
//freopen("dinner.in","r",stdin);
//freopen("dinner.out","w",stdout);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=2;j++)
{
scanf("%d",&a[i][j]);
}
scanf("%d",&c[i]);
}
f[1][1]=a[1][1]+c[1];
f[1][2]=a[1][2];
for(int i=2;i<=n;i++)
{
for(int j=1;j<=2;j++)
{
int minnum=min(f[i-1][1],f[i-1][2]);
f[i][j]=min(minnum+c[i],f[i-1][j])+a[i][j];
}
}
int ans=min(f[n][1],f[n][2]);
printf("%d",ans);
}T3 乐高山上的士兵
我说我也不会!!!
我连子集和都WA……(逃
等我写出正解再更新
———-过去式(时?)
终于写出了正解;
总结T3开始
考查知识点:DFS
题目大意:
提供一个地图,在此地图中找到山顶的个数。(注:一个山顶是由一个或者多个连续的点构成的,并且与山顶相连的点的高度都小于山顶的高度。如果两个点相连,则这两个点的行的差都不超过 1,列的差也不超过 1。当然高度为0表示地面,不能称之为山顶。)
考试的时候就蒙了,因为自己本身DFS就不太懂(废话连子集和都WA)就逼着自己去做,但是最后也没有写出来,只好打了一个有着极大漏洞的,非DFS的暴力,拿了20分;
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
int f[200][200];
int nmp[200][200];
int a[9]={0,-1,-1,-1,0,1,1,1,0};
int b[9]={0,-1,0,1,1,1,0,-1,-1};
int ans;
void search(int x,int y)
{
int k=0;
for(int i=1;i<=8;i++)
{
if(f[x+a[i]][y+b[i]]==f[x][y])
{
nmp[x+a[i]][y+b[i]]=1;
}
if(f[x+a[i]][y+b[i]]>f[x][y])
{
k=1;
}
}
if(k==1)
{
return ;
}
if(nmp[x][y]==0)
{
ans++;
}
return ;
}
int main()
{
freopen("lego.in","r",stdin);
freopen("lego.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&f[i][j]);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(f[i][j]!=0)
{
search(i,j);
}
}
}
printf("%d",ans);
}在赛后让Ciel和Tonyzhao指导了一番,发现都有着自己的思路:
是什么呢?是什么呢?是什么呢?
具体在章末会提到(逃
回归主题:
对于一个点是不是山峰,必须满足以下要点:
1:这个点高度大于0;
2:这个点本身周围不能有别的点高度比它大;
3:若周围有高度和它相同的点,必须要同时满足那个点也满足条件2;
因为我们无法一次性扫出全部的,和它相同高度的点是否都满足条件,
所以:DFS就派上了用场;
还需要注意DFS时的边界问题,并且要判重(要不然就死递归了);
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
int f[200][200];//存图
int nmp[200][200];//判断一个点是否被DFS过
int a[9]={0,-1,-1,-1,0,1,1,1,0};
int b[9]={0,-1,0,1,1,1,0,-1,-1};
int ans;
int search(int x,int y)
{
nmp[x][y]=1;
int tmp=1;
for(int i=1;i<=8;i++)
{
int dx=x+a[i];
int dy=y+b[i];
if(dx>0&&dx<=n&&dy>0&&dy<=m)
{
if(f[dx][dy]>f[x][y])
{
tmp=0;
}
if(f[dx][dy]==f[x][y]&&nmp[dx][dy]==0)
{
tmp=tmp&search(dx,dy);
}
}
}
return tmp;
}
int main()
{
freopen("lego.in","r",stdin);
freopen("lego.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&f[i][j]);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(f[i][j]!=0)
{
if(nmp[i][j]==0)
{
if(search(i,j)==1)
{
ans++;
}
}
}
}
}
printf("%d",ans);
}附上Ciel AC代码
#include <cstdio>
#include <algorithm>
using namespace std;
int n,m,a[110][110],cnt;
int dx[9]={0,-1,0,1,-1,1,-1,0,1},dy[9]={0,-1,-1,-1,0,0,1,1,1};
bool b[110][110];
int DFS(int x,int y)
{
int rtn=1;//如果一路检测没有出现问题则是山峰
b[x][y]=1;//标记已经扫描过
if(x<1||y<1||x>n||y>m)return true;//防止溢出边界
for(int k=1;k<=8;k++)
{
if(a[x+dx[k]][y+dy[k]]>a[x][y])rtn=0;//如果周围某个点比它本身高,则它本身不是山峰
else if(a[x+dx[k]][y+dy[k]]==a[x][y]&&!b[x+dx[k]][y+[k]]) rtn&=DFS(x+dx[k],y+dy[k]);
//如果等高,则这个点必须是山峰一部分,如果没有扫过则递归判断它
}
return rtn;
}
int main()
{
freopen("lego.in","r",stdin);
freopen("lego.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)
if(a[i][j]&(b[i][j]^1)&DFS(i,j))cnt++;
//条件等价于(a[i][j]!=0&&b[i][j]==false&&DFS(i,j)==1)
//如果没计算过且成立则计山峰
printf("%d",cnt);
return 0;
}