Description
huyichen世子事件后,xuzhenyi成了皇上特聘的御前一品侍卫。 皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状;某些宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。 可是xuzhenyi手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。 帮助xuzhenyi布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
Input
输入文件中数据表示一棵树,描述如下: 第1行 n,表示树中结点的数目。 第2行至第n+1行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号i(0< i< =n),在该宫殿安置侍卫所需的经费k,该边的儿子数m,接下来m个数,分别是这个节点的m个儿子的标号r1,r2,...,rm。 对于一个n(0 < n < = 1500)个结点的树,结点标号在1到n之间,且标号不重复。
Output
输出文件仅包含一个数,为所求的最少的经费。
Sample Input
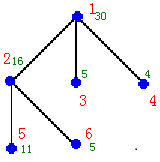
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0Sample Output
25HINT
题目分析
典型的带权最小支配集
fa[x]表示由自己父亲节点支配自己
self[x]表示由自己支配自己
son[x]表示由某一个子节点支配自己
分析:
如果是父亲节点支配自己 那么子节点只有(自己)支配自己或者(子节点的子节点)来支配自己
如果是自身支配自己 那么子节点不论怎样都可以
如果是子节点支配自己的话 那就选一个最小的self[y] 剩下的子节点可以(自己)支配自己或者(子节点的子节点)来支配自己
转移方程:令x是y的father
fa[x]=Σmin(self[y],son[y]);
self[x]=val[x]+Σmin(self[y],min(son[y],fa[y]));
son[x]=min self[z]+Σmin(son[y],self[y])(y!=z);
最后记得选用一个入度为0的点为树根
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,root,tot;
int ru[1600];
int head[1600],net[1600],to[1600];
int val[1600],self[1600],son[1600],fa[1600];
void dfs(int x)
{
self[x]=val[x];
int tmp=0x7f7f7f7f;
for(int i=head[x];i;i=net[i])
{
dfs(to[i]);
self[x]+=min(self[to[i]],min(son[to[i]],fa[to[i]]));
fa[x]+=min(self[to[i]],son[to[i]]);
son[x]+=min(son[to[i]],self[to[i]]);
tmp=min(self[to[i]]-son[to[i]],tmp);
}
if(tmp>0)son[x]+=tmp;
return ;
}
void add(int x,int y)
{
net[++tot]=head[x];
to[tot]=y;
head[x]=tot;
}
int find_root()
{
for(int i=1;i<=n;i++)
if(!ru[i]) return i;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
scanf("%d%d",&val[x],&m);
for(int i=1;i<=m;i++)
{
int tmp;
scanf("%d",&tmp);
add(x,tmp);
ru[tmp]++;
}
}
root=find_root();
dfs(root);
printf("%d",min(self[root],son[root]));
}
