题目传送门

Description

在 W 星球上有 n 个国家。为了各自国家的经济发展，他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬，他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如，在下图中，虚线所示道路两端分别有 2 个、4 个国家，如果该道路长度为 1，则费用为 1×|2–4|=2。图中圆圈里的数字表示国 家的编号。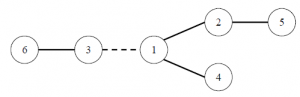

由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建 费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计 算出所需要的费用。请你帮助国王们设计一个这样的软件。

Input

输入的第一行包含一个整数 n，表示W星球上的国家的数量，国家从1到n编号。接下来n–1行描述道路建设情况，其中第i行包含三个整数ai、bi和 ci，表 示第i条双向道路修建在ai与bi两个国家之间长度为ci。

Output

输出一个整数，表示修建所有道路所需要的总费用。

Sample Input

6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1

Sample Output

20

HINT

题目分析：

                           这是一道卡常数的题

这个题说实话很水 大多数人都能一眼看出这道题是搜索
对于每条道路 都会有父亲节点 和儿子节点
我们记录每一个点的子树大小 size[x]
所以

但是本题的关键是：DFS会爆栈 所以我们转用BFS来求解
那么如何用BFS来求解子树大小呢？
我们引入BFS序这个东西，和DFS序一样  它是一个保存BFS搜索顺序的序列
有了BFS序 我们可以从叶子结点x往回推 利用size[x]对每个fa_x的子树大小做出贡献
然后枚举每条边累加答案即可

但是这样做时间很长 在洛谷上AC后 在JDOJ上TLE 85%(1516ms)
先来%一下JDOJ的数据......

首先听取了老师的建议，使用了 数组模拟队列+读入优化

事实证明这么做很有效果  在JDOJ上TLE 15%(1220ms) 时间骤减

那么 我们来想想在方法上的优化

在我们刚才的做法中，枚举每条边花费了很多时间，我们能不能换一种方式呢？
注意我们用来计算的公式和size[fa_x]并没有关系 因为对于所有的边来说，to[i]是唯一的 那么我们就可以保存 对于每个to[i]的边的权值 在计算size的时候就可以直接出解了

改变方法后 在 JDOJ上TLE 10% (1036ms)

现在就剩下微小的常数了

我们来观察读入优化的代码

int read()
{
    int sum=0;
    char c;
    c=getchar();
    while(c==' '||c=='\n')
        c=getchar();
    while(c<='9'&&c>='0')
        sum=sum*10+(c-'0'),c=getchar();
    return sum;
}

因为 sum*10=(sum<<3)+(sum<<1) 所以我们能用位运算加速？？

闷声改完 顺便将BFS时的to[i]用nmp变量代替了一下 ←(迷之顺便)

然后再交 AC辣！(988ms)

然而这究竟是位运算加速还是nmp代替调用次数的锅？
尝试ing......

亲测:只有两个都用上的时候才有效

无位运算:1188ms   无nmp:1120ms

这个题AC的很迷啊...... NOI的题都好强

最后附上AC代码

#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
int n,tot;
int next[2000100];
int head[1000100];
int to[2000100];
int size[1000100];
int a[1000100];
int fa[1000100];
bool vis[1000100];
int val[2000100];
void add(int x,int y,int v)
{
    next[++tot]=head[x];
    to[tot]=y;
    val[tot]=v;
    head[x]=tot;
}
int read()
{
    int sum=0;
    char c;
    c=getchar();
    while(c==' '||c=='\n')
        c=getchar();
    while(c<='9'&&c>='0')
        sum=(sum<<3)+(sum<<1)+(c-'0'),c=getchar();
    return sum;
}
int que[1000100];
long long sum[1000100];
int l=1,r;
void bfs()
{
    vis[1]=true;
    que[++r]=1;
    while(l<=r)
    {
        int tmp=que[l++];
        a[++a[0]]=tmp;
        size[tmp]=1;
        for(int i=head[tmp];i;i=next[i])
        {
            int nmp=to[i];
            if(!vis[nmp])
            {
                fa[nmp]=tmp;
                vis[nmp]=true;
                que[++r]=nmp;
                sum[nmp]=val[i];
            }
        }
    }
}
long long Absnumber(long long x)
{
    return x<0?-x:x;
}
long long ans;
void work()
{
    for(int i=a[0];i>=1;i--)
    {
        size[fa[a[i]]]+=size[a[i]];
        long long tmp=Absnumber(n-size[a[i]]*2);
        ans+=(tmp*sum[a[i]]);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        int x,y,c;
        x=read();
        y=read();
        c=read();
        add(x,y,c);
        add(y,x,c);
    }
    bfs();
    work();
    printf("%lld",ans);
}