Description
Ali is Hamed's little brother and tomorrow is his birthday. Hamed wants his brother to earn his gift so he gave him a hard programming problem and told him if he can successfully solve it, he'll get him a brand new laptop. Ali is not yet a very talented programmer like Hamed and although he usually doesn't cheat but this time is an exception. It's about a brand new laptop. So he decided to secretly seek help from you. Please solve this problem for Ali.
An n-vertex weighted rooted tree is given. Vertex number 1 is a root of the tree. We define d(u, v) as the sum of edges weights on the shortest path between vertices u and v. Specifically we define d(u, u) = 0. Also let's define S(v) for each vertex v as a set containing all vertices u such that d(1, u) = d(1, v) + d(v, u). Function f(u, v) is then defined using the following formula:
The goal is to calculate f(u, v) for each of the q given pair of vertices. As the answer can be rather large it's enough to print it modulo + 7.
给你一棵树,个点,条边,边有边权,每次给你两个点,,设为点与点之间的距离,点集为点的子树内所有点的集合,询问
Input
In the first line of input an integer n (1 ≤ n ≤ 105), number of vertices of the tree is given.
In each of the next n - 1 lines three space-separated integers ai, bi, ci (1 ≤ ai, bi ≤ n, 1 ≤ ci ≤ 109) are given indicating an edge between ai and bi with weight equal to ci.
In the next line an integer q (1 ≤ q ≤ 105), number of vertex pairs, is given.
In each of the next q lines two space-separated integers ui, vi (1 ≤ ui, vi ≤ n) are given meaning that you must calculate f(ui, vi).
It is guaranteed that the given edges form a tree.
Output
Output q lines. In the i-th line print the value of f(ui, vi) modulo 109 + 7.
input
5
1 2 1
4 3 1
3 5 1
1 3 1
5
1 1
1 5
2 4
2 1
3 5
output
10
1000000005
1000000002
23
1000000002
input
8
1 2 100
1 3 20
2 4 2
2 5 1
3 6 1
3 7 2
6 8 5
6
1 8
2 3
5 8
2 6
4 7
6 1
output
999968753
49796
999961271
999991235
999958569
45130
题目分析
丧心病狂推式子系列
来我们一步一步讲
假设我们现在什么都知道(大雾) 我们对两个点的相对位置关系进行分类讨论:
这棵树长成这个样子: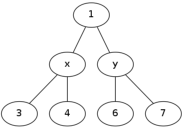
......
通过观察可以发现,这时的
好打住... 式子推到这里就可以暂停了 怎样计算待会再细说
这棵树长成这个样子: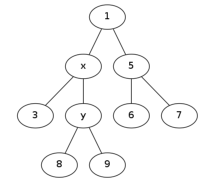
......
通过观察可以发现,这时的
好啊 它和上个情况的式子长得一样(然而并没有什么卵用)
式子推到这里就可以暂停了 怎样计算待会再细说*2
这棵树长成这个样子: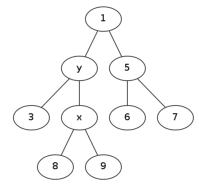
......
通过观察可以发现,这时的
好打住... 式子推到这里就可以暂停了 怎样计算待会再细说现在来讲......
首先 我们来化简
这个式子
好的 我们将展开的结果代入上面的最终式子,发现,我们只要求出下面几个东西,上面的式子就可以出解了
并且
并且
啊♂ 所以我们只需要在时间内求出4个东西就好了
这个东西能树形DP解决 那就愉快的做完了
我把考试题改为3次方真是丧心病狂
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
int n,m,tot;
int head[100010],to[300010],net[300010];
long long val[300010],mod=1000000007;
void add(int x,int y,int c)
{
net[++tot]=head[x],head[x]=tot,to[tot]=y,val[tot]=c;
}
int deep[100010],size[100010],son[100010],fa[100010],top[100010];
struct your
{
long long dis,sqr;
}dp[100010],sum[100010],all[100010];
long long dis[100010];
void dfs(int x)
{
deep[x]=deep[fa[x]]+1,size[x]=1;
for(int i=head[x];i;i=net[i])
if(to[i]!=fa[x])
{
dis[to[i]]=(dis[x]+val[i])%mod,fa[to[i]]=x,dfs(to[i]),size[x]+=size[to[i]];
if(size[to[i]]>size[son[x]]) son[x]=to[i];
dp[x].dis=(dp[x].dis+dp[to[i]].dis%mod+(long long) size[to[i]]*val[i]%mod)%mod;
long long tmp=(long long) size[to[i]]*val[i]%mod*val[i]%mod;
long long nmp=(dp[to[i]].sqr+2*val[i]*dp[to[i]].dis%mod)%mod;
dp[x].sqr=(dp[x].sqr+tmp+nmp)%mod;
}
}
void dfs2(int x)
{
for(int i=head[x];i;i=net[i])
{
if(to[i]==fa[x]) continue;
long long tmp=(sum[x].dis+(long long)(n-2*size[to[i]])*val[i])%mod;
long long nmp=(dp[x].dis-dp[to[i]].dis+mod)%mod;
sum[to[i]].dis=(tmp+nmp)%mod;
tmp=(sum[x].sqr+2*sum[x].dis*val[i]%mod+(long long) (n-size[x])*val[i]%mod*val[i]%mod)%mod;
long long dx,dy,dc;
dx=((dp[x].sqr-dp[to[i]].sqr-2*val[i]*dp[to[i]].dis%mod-(long long) size[to[i]]*val[i]%mod*val[i]%mod)%mod+mod)%mod;
dy=(long long)(size[x]-size[to[i]])*val[i]%mod*val[i]%mod;
dc=(2*val[i]*(dp[x].dis-dp[to[i]].dis-(long long) val[i]*size[to[i]]%mod )%mod+mod)%mod;
sum[to[i]].sqr=(tmp+dx+dy+dc)%mod;
dfs2(to[i]);
}
}
void dfs3(int x,int temp)
{
top[x]=temp;
if(son[x]) dfs3(son[x],temp);
for(int i=head[x];i;i=net[i])
if(to[i]!=fa[x]&&to[i]!=son[x]) dfs3(to[i],to[i]);
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
return deep[x]<deep[y]?x:y;
}
void check(int x,int y);
int main()
{
scanf("%d",&n);
for(int x,y,c,i=1;i<n;i++)
scanf("%d%d%d",&x,&y,&c),add(x,y,c),add(y,x,c);
dfs(1),dfs2(1),dfs3(1,1);
for(int i=1;i<=n;i++)
{
all[i].dis=(sum[i].dis+dp[i].dis)%mod;
all[i].sqr=(sum[i].sqr+dp[i].sqr)%mod;
}
scanf("%d",&m);
for(int x,y,i=1;i<=m;i++)
scanf("%d%d",&x,&y),check(x,y);
return 0;
}
void check(int x,int y)
{
int l=lca(x,y);
if(l!=x&&l!=y)
{
long long c=((dis[x]+dis[y]-2*dis[l])%mod+mod)%mod;
long long tmp=(dp[y].sqr+(long long) c*c%mod*size[y]%mod+2*c*dp[y].dis%mod)%mod;
printf("%lld\n",(2*tmp%mod-all[x].sqr+mod)%mod );
}
else if(l==x)
{
long long c=((dis[x]+dis[y]-2*dis[l])%mod+mod)%mod;
long long tmp=(dp[y].sqr+(long long) c*c%mod*size[y]%mod+2*c*dp[y].dis%mod)%mod;
printf("%lld\n",(2*tmp%mod-all[x].sqr+mod)%mod );
}
else if(l==y)
{
long long c=((dis[x]+dis[y]-2*dis[l])%mod+mod)%mod;
long long tmp=(sum[y].sqr+(long long) c*c%mod*(n-size[y])%mod+2*c*sum[y].dis%mod)%mod;
printf("%lld\n",((all[x].sqr-2*tmp)%mod+mod)%mod);
}
}
啊 三次方和二次方一样嘛
三次方代码:
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
int m,tot;
long long n;
int head[100010],to[300010],net[300010];
long long val[300010],P=1000000007;
void add(int x,int y,int c)
{
net[++tot]=head[x],head[x]=tot,to[tot]=y,val[tot]=c;
}
int deep[100010],son[100010],fa[100010],top[100010];
struct your
{
long long dis,sqr,tre;
}dp[100010],sum[100010],all[100010];
long long dis[100010],size[100010];
void dfs(int x)
{
long long tmp,nmp;
deep[x]=deep[fa[x]]+1,size[x]=1;
for(int i=head[x];i;i=net[i])
{
if(to[i]==fa[x]) continue;
dis[to[i]]=(dis[x]+val[i])%P,fa[to[i]]=x,dfs(to[i]),size[x]+=size[to[i]];
if(size[to[i]]>size[son[x]]) son[x]=to[i];
dp[x].dis=(dp[x].dis+dp[to[i]].dis%P+size[to[i]]*val[i]%P)%P;
tmp=size[to[i]]*val[i]%P*val[i]%P;
nmp=(dp[to[i]].sqr+2*val[i]*dp[to[i]].dis%P)%P;
dp[x].sqr=(dp[x].sqr+tmp+nmp)%P;
tmp=size[to[i]]%P*val[i]%P*val[i]%P*val[i]%P;
nmp=(3*val[i]%P*dp[to[i]].sqr%P+3*val[i]*val[i]%P*dp[to[i]].dis%P)%P;
dp[x].tre=(dp[x].tre+tmp+nmp+dp[to[i]].tre)%P;
}
}
void dfs2(int x)
{
long long dx,dy,dc,tmp,nmp;
for(int i=head[x];i;i=net[i])
{
if(to[i]==fa[x]) continue;
tmp=(sum[x].dis+(n-2*size[to[i]])*val[i])%P;
nmp=(dp[x].dis-dp[to[i]].dis+P)%P;
sum[to[i]].dis=(tmp+nmp)%P;
tmp=(sum[x].sqr+2*sum[x].dis*val[i]%P+(n-size[x])*val[i]%P*val[i]%P)%P;
dx=((dp[x].sqr-dp[to[i]].sqr-2*val[i]*dp[to[i]].dis%P-size[to[i]]*val[i]%P*val[i]%P)%P+P)%P;
dy=(2*val[i]*(dp[x].dis-dp[to[i]].dis-val[i]*size[to[i]]%P)%P+P)%P;
dc=(size[x]-size[to[i]])*val[i]%P*val[i]%P;
sum[to[i]].sqr=(tmp+dx+dy+dc)%P;
tmp=(sum[x].tre+3*val[i]*sum[x].sqr%P+3*val[i]*val[i]%P*sum[x].dis%P+(n-size[x])*val[i]%P*val[i]%P*val[i]%P)%P;
dx=((dp[x].tre-dp[to[i]].tre-3*val[i]*dp[to[i]].sqr%P-3*val[i]*val[i]%P*dp[to[i]].dis%P-size[to[i]]*val[i]%P*val[i]%P*val[i]%P)%P+P)%P;
dy=3*val[i]*(((dp[x].sqr-dp[to[i]].sqr-2*val[i]*dp[to[i]].dis%P-size[to[i]]*val[i]%P*val[i]%P)%P+P)%P)%P;
dc=(3*val[i]*val[i]%P*(dp[x].dis-dp[to[i]].dis-val[i]*size[to[i]]%P)%P+P)%P;
nmp=(size[x]-size[to[i]])*val[i]%P*val[i]%P*val[i]%P;
sum[to[i]].tre=(tmp+dx+dy+dc+nmp)%P;
dfs2(to[i]);
}
}
void dfs3(int x,int temp)
{
top[x]=temp;
if(son[x]) dfs3(son[x],temp);
for(int i=head[x];i;i=net[i])
if(to[i]!=fa[x]&&to[i]!=son[x]) dfs3(to[i],to[i]);
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]]) swap(x,y);
x=fa[top[x]];
}
return deep[x]<deep[y]?x:y;
}
void check(int x,int y);
int main()
{
freopen("distance.in","r",stdin);
freopen("distance.out","w",stdout);
scanf("%lld",&n);
for(int x,y,c,i=1;i<n;i++)
scanf("%d%d%d",&x,&y,&c),add(x,y,c),add(y,x,c);
dfs(1),dfs2(1),dfs3(1,1);
for(int i=1;i<=n;i++)
{
all[i].dis=(sum[i].dis+dp[i].dis)%P;
all[i].sqr=(sum[i].sqr+dp[i].sqr)%P;
all[i].tre=(sum[i].tre+dp[i].tre)%P;
}
scanf("%d",&m);
for(int x,y,i=1;i<=m;i++)
scanf("%d%d",&x,&y),check(x,y);
fclose(stdin);
fclose(stdout);
return 0;
}
void check(int x,int y)
{
int l=lca(x,y);
if(l!=x&&l!=y)
{
long long c=((dis[x]+dis[y]-2*dis[l])%P+P)%P;
long long tmp=(dp[y].tre+3*c%P*dp[y].sqr%P+3*c%P*c%P*dp[y].dis%P+size[y]*c%P*c%P*c%P)%P;
printf("%lld\n",(2*tmp%P-all[x].tre+P)%P);
}
else if(l==x)
{
long long c=((dis[x]+dis[y]-2*dis[l])%P+P)%P;
long long tmp=(dp[y].tre+3*c%P*dp[y].sqr%P+3*c%P*c%P*dp[y].dis%P+size[y]*c%P*c%P*c%P)%P;
printf("%lld\n",(2*tmp%P-all[x].tre+P)%P);
}
else if(l==y)
{
long long c=((dis[x]+dis[y]-2*dis[l])%P+P)%P;
long long tmp=(sum[y].tre+3*c%P*sum[y].sqr%P+3*c%P*c%P*sum[y].dis%P+(n-size[y])*c%P*c%P*c%P)%P;
printf("%lld\n",((all[x].tre-2*tmp)%P+P)%P);
}
}
