Description
A little girl loves problems on trees very much. Here's one of them.
A tree is an undirected connected graph, not containing cycles. The degree of node x in the tree is the number of nodes y of the tree, such that each of them is connected with node x by some edge of the tree.
Let's consider a tree that consists of n nodes. We'll consider the tree's nodes indexed from 1 to n. The cosidered tree has the following property: each node except for node number 1 has the degree of at most 2.
Initially, each node of the tree contains number 0. Your task is to quickly process the requests of two types:
- Request of form: 0 v x d. In reply to the request you should add x to all numbers that are written in the nodes that are located at the distance of at most d from node v. The distance between two nodes is the number of edges on the shortest path between them.
- Request of form: 1 v. In reply to the request you should print the current number that is written in node v.
题意:
给出一颗树,每次对树进行两种操作。
第一种操作:给节点v及距离节点v,d个单位长度以内的节点加x
第二种操作:询问节点v当前的值。
注意:给出的树中,除了节点1以为,其他节点的度都不会超过2。
Input
The first line contains integers n (2 ≤ n ≤ 105) and q (1 ≤ q ≤ 105) — the number of tree nodes and the number of requests, correspondingly.
Each of the next n - 1 lines contains two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi), that show that there is an edge between nodes uiand vi. Each edge's description occurs in the input exactly once. It is guaranteed that the given graph is a tree that has the property that is described in the statement.
Next q lines describe the requests.
- The request to add has the following format: 0 v x d (1 ≤ v ≤ n, 1 ≤ x ≤ 104, 1 ≤ d < n).
- The request to print the node value has the following format: 1 v (1 ≤ v ≤ n).
The numbers in the lines are separated by single spaces.
Output
For each request to print the node value print an integer — the reply to the request.
Sample Input
3 6
1 2
1 3
0 3 1 2
0 2 3 1
0 1 5 2
1 1
1 2
1 3Sample Output
9
9
6题目分析:
能够A这道题我觉得我十分幸运
这棵树除了点1以外 其余的点的度数都不超过2 而每个非点必须要有一个父亲..所以每个非根节点至多一个孩子
所以这棵树一定是这样的:
对于更新点权有两种情况
- 更新的点的上界不超过这条链 那么直接修改就可以
- 更新的点的上界超出了这条链 那么其余的链都需要更新
单链的修改使用一颗线段树维护 时间是O(log n)
然而情况2对于某些图 例如菊花图 循环修改链的时间是O(n*m) 妥妥TLE
那么我们再维护一个深度的线段树:修改就像这个样子:
当更新超过了单链的时候 超出链的部分就直接在维护深度的线段树里更新
比方说这里想要更新红色的部分 那么就把它分为黄色和红色两部分来更新
因为每条链的长度不知道 并且极限情况[10^5][10^5]爆内存 所以用vector 写线段树 动态申请空间
正常的话 这道题到这里就结束了
然而..... 然而.... 我会用vector 写线段树么QAQ
很显然我不会啊......
先不管1 我们想如何只用一颗线段树来维护所有的链:
deep[] :每个点的深度
num[] :每个点在哪条链上
maxlian[] :每条链最大的深度(每条链有多少个点)
sumlian[] :1~i-1 的链的总点数
numdeep[] :每个深度都有多少点
sumdeep[] :1~i的深度的总点数
wheredeep[] :每个点在自己所处的深度中是第几个
用以上的东西 就能快速求出每个点 在链线段树和深度线段树中的位置 并实现查询和更新
例如:
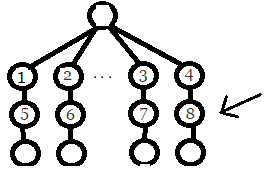
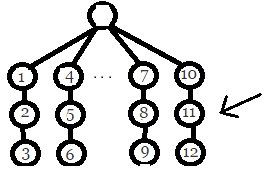
对于箭头指的点 在深度线段树里是8 在链线段树里是11
细节神TM多 看代码吧
最后 单开一个变量记录1的权值 就可以了
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int n,m;
int net[300100],to[300100],head[300100];
int val;
int tot;
void add(int x,int y)
{
net[++tot]=head[x];
to[tot]=y;
head[x]=tot;
}
int tmp;
int cnt;//sum of lian
int top;//sum of deep
int deep[100100];
int num[100100];//number of lian
int maxlian[100100];//maxlian of each lian
int sumlian[100100];//sigma 1~i-1 maxlian[]
int numdeep[100100];//number of each deep
int sumdeep[100100];//sigma 1~i numdeep[]
int wheredeep[101000];//where is the i in its numdeep
void dfs(int x,int temp,int color)
{
deep[x]=deep[temp]+1;
numdeep[deep[x]]++;
wheredeep[x]=numdeep[deep[x]];
num[x]=color;
tmp=max(deep[x],tmp);
for(int i=head[x];i;i=net[i])
if(to[i]!=temp) dfs(to[i],x,color);
}
void check(int x,int y,int c);
struct tree
{
struct your
{
int x,y;
int add,sum;
}a[1000100];
void build(int dx,int dy,int num)
{
a[num].x=dx,a[num].y=dy;
if(dx==dy) return ;
int mid=(dx+dy)>>1;
build(dx,mid,num<<1);
build(mid+1,dy,num<<1|1);
}
void pushdown(int num)
{
a[num<<1].add+=a[num].add;
a[num<<1|1].add+=a[num].add;
a[num<<1].sum+=a[num].add*(a[num<<1].y-a[num<<1].x+1);
a[num<<1|1].sum+=a[num].add*(a[num<<1|1].y-a[num<<1|1].x+1);
a[num].add=0;
}
void update(int dx,int dy,int c,int num)
{
if(dx==0||dy==0) return ;
if(a[num].x==dx&&a[num].y==dy)
{
a[num].sum+=c*(a[num].y-a[num].x+1);
a[num].add+=c;
return;
}
if(a[num].add) pushdown(num);
int mid=(a[num].x+a[num].y)>>1;
if(dx>mid) update(dx,dy,c,num<<1|1);
else if(dy<=mid) update(dx,dy,c,num<<1);
else
{
update(dx,mid,c,num<<1);
update(mid+1,dy,c,num<<1|1);
}
a[num].sum=a[num<<1].sum+a[num<<1|1].sum;
}
int ask(int dx,int num)
{
if(dx==0) return 0;
if(a[num].x==dx&&a[num].y==dx)
return a[num].sum;
if(a[num].add) pushdown(num);
int mid=(a[num].x+a[num].y)>>1;
if(dx<=mid) return ask(dx,num<<1);
return ask(dx,num<<1|1);
}
}A,B;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y),add(y,x);
}
for(int i=head[1];i;i=net[i])
{
tmp=0,cnt++;
dfs(to[i],1,cnt);
maxlian[cnt]=tmp;
top=max(top,tmp);
}
A.build(1,n,1);
B.build(1,n,1);
for(int i=1;i<=top;i++) sumdeep[i]=sumdeep[i-1]+numdeep[i];
for(int i=1;i<=cnt;i++) sumlian[i]=sumlian[i-1]+maxlian[i-1];
for(int i=1;i<=m;i++)
{
int tmp;
scanf("%d",&tmp);
if(!tmp)
{
int x,y,c;
scanf("%d%d%d",&x,&c,&y);
check(x,c,y);
}
else
{
int x;
scanf("%d",&x);
if(x==1) printf("%d\n",val);
else printf("%d\n",A.ask(sumlian[num[x]]+deep[x],1)+B.ask(sumdeep[deep[x]-1]+wheredeep[x],1));
}
}
return 0;
}
void check(int x,int c,int y)
{
if(x==1)
{
val+=c;
B.update(1,sumdeep[min(top,y)],c,1);
return ;
}
if(deep[x]>=y)
{
if(deep[x]==y)
{
val+=c;
A.update(sumlian[num[x]]+1,sumlian[num[x]]+min(maxlian[num[x]],deep[x]+y),c,1);
return ;
}
A.update(sumlian[num[x]]+deep[x]-y,sumlian[num[x]]+min(maxlian[num[x]],deep[x]+y),c,1);
}
else
{
val+=c;
B.update(1,sumdeep[min(top,y-deep[x])],c,1);
if(top<=y-deep[x]) return ;
if(y-deep[x]+1>maxlian[num[x]]) return ;
A.update(sumlian[num[x]]+y-deep[x]+1,sumlian[num[x]]+min(maxlian[num[x]],deep[x]+y),c,1);
}
}

