题目描述

Description

一次舞会有n个男孩和n个女孩。每首曲子开始时，所有男孩和女孩恰好配成n对跳交谊舞。每个男孩都不会和同一个女孩跳两首（或更多）舞曲。有一些男孩女孩相互喜欢，而其他相互不喜欢（不会“单向喜欢”）。每个男孩最多只愿意和k个不喜欢的女孩跳舞，而每个女孩也最多只愿意和k个不喜欢的男孩跳舞。给出每对男孩女孩是否相互喜欢的信息，舞会最多能有几首舞曲？

Input

第一行包含两个整数n和k。以下n行每行包含n个字符，其中第i行第j个字符为'Y'当且仅当男孩i和女孩j相互喜欢。

Output

仅一个数，即舞曲数目的最大值。

Sample Input

3 0
YYY
YYY
YYY

Sample Output

3

HINT

N<=50 K<=30

题目分析

二分+最大流
对每个人拆点 i i'

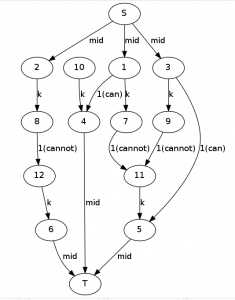
大体就这个意思 上面的图不全
每次二分判断是否满流即可

#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
int n,m,ans;
int tot=1,head[2100],to[800010],net[800010],val[800010];
int s,t;
void add(int x,int y,int c)
{
    net[++tot]=head[x],head[x]=tot,to[tot]=y,val[tot]=c;
    net[++tot]=head[y],head[y]=tot,to[tot]=x,val[tot]=0;
}
int dis[80010];
int bfs()
{
    queue<int>q;
    memset(dis,0,sizeof dis);
    q.push(s);
    dis[s]=1;
    while(q.size())
    {
        int nmp=q.front();
        q.pop();
        for(int i=head[nmp];i;i=net[i])
            if(val[i]>0&&!dis[to[i]])
            {
                dis[to[i]]=dis[nmp]+1;
                q.push(to[i]);
                if(to[i]==t) return 1;
            }
    }
    return 0;
}
int dinic(int x,int flow)
{
    int tmp,temp=flow;
    if(x==t) return flow;
    for(int i=head[x];i;i=net[i])
        if(val[i]>0&&dis[to[i]]==dis[x]+1)
        {
            tmp=dinic(to[i],min(val[i],temp));
            if(tmp==0) dis[to[i]]=0;
            temp-=tmp,val[i]-=tmp,val[i^1]+=tmp;
            if(!temp) break;
        }

    return flow-temp;
}
char sa[100];
bool can[100][100];
int check(int mid)
{ 
    s=0,t=4*n+1;
    tot=1;
    memset(head,0,sizeof head);
    for(int i=1;i<=n;i++) add(s,i,mid);
    for(int i=1;i<=n;i++) add(i+n,t,mid);
    for(int i=1;i<=n;i++) add(i,i+2*n,m);
    for(int i=n+1;i<=n*2;i++) add(i+2*n,i,m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            if(can[i][j]) add(i,j+n,1);
            else add(i+2*n,j+n*3,1);
        }
    int sum=0;
    while(bfs()) sum+=dinic(s,1<<30);
    return sum>=mid*n;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",&sa[0]);
        for(int j=0;j<n;j++)
            can[i][j+1]=(sa[j]=='Y')?1:0;
    }
    int l=0,r=n,sum=0,mid;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(check(mid)) sum=mid,l=mid+1;
        else r=mid-1;
    }
    printf("%d",sum);
    return 0;
}