题目描述

Description

给你一个式子 求第n项%g   Xn+1=(a∗Xn+c) mod m 

HINT

n<=10¹⁸,m.a.c.x0 <=10¹⁸ g<=10⁸

题目分析：

裸的矩阵乘法快速幂 为了防止溢出还要用上快速加

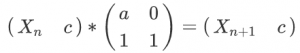
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
long long m,tmp,c,xx,n,g;
long long a[3][3],f[3];
long long tmp1,tmp2,tmp3,tmp4;
void init()
{
    f[1]=xx;
    f[2]=c;
    a[1][1]=tmp;
    a[1][2]=0;
    a[2][1]=1;
    a[2][2]=1;
}
long long ksj(long long x,long long y)
{
    long long sum=0;
    while(y)
    {
        if(y&1)sum=(sum+x)%m;
        y>>=1;
        x=(x+x)%m;
    }
    return sum;
}
void ksm(long long x)
{
    while(x)
    {
        if(x&1)
        {
            tmp1=ksj(f[1],a[1][1])+ksj(f[2],a[2][1]);
            tmp2=ksj(f[1],a[1][2])+ksj(f[2],a[2][2]);
            f[1]=tmp1%m;
            f[2]=tmp2%m;
        }
        x>>=1;
        tmp1=ksj(a[1][1],a[1][1])+ksj(a[1][2],a[2][1]);
        tmp2=ksj(a[1][1],a[1][2])+ksj(a[1][2],a[2][2]);
        tmp3=ksj(a[2][1],a[1][1])+ksj(a[2][2],a[2][1]);
        tmp4=ksj(a[2][1],a[1][2])+ksj(a[2][2],a[2][2]);
        a[1][1]=tmp1%m;
        a[1][2]=tmp2%m;
        a[2][1]=tmp3%m;
        a[2][2]=tmp4%m;
    }
}
int main()
{
    scanf("%lld%lld%lld%lld%lld%lld",&m,&tmp,&c,&xx,&n,&g);
    init();
    ksm(n);
    printf("%lld",f[1]%m%g);
    return 0;
}