T1 敬业福
题目大意:
在一个 N*N 的矩阵中,填满了正整数和一个零,零的位置表示一个空位置,问这个位置填多少才能 满足每行的和与每列的和都是一个定值。注意:数据保证一定会有且只有一个空位置。
输入:
第一行一个正整数 N。 接下来 N 行,每行 N 个由空格隔开的数字。
输出:
一行一个整数,如果存在满足条件的唯一正整数的话,输出这个正整数。否则,如果无解、解为负值,解为零,存在多个解,输出-1.
Input
3
1 1 1
1 0 1
1 1 1Output
1
数据范围:
1<=N<=500 设 Aij 为第 i 行第 j 列的数字 0<=Aij<=10^9
题目分析:
这道题就是纯模拟 主要难点是判断什么时候输出'-1'
- 当N==1时,即只有一个空位置,填任意正整数都合理,所以属于多解的情况。
- 当空位置的值为负时,需要特判。
- 在不包含空位置的行中,有两行或者两行以上的和不相等的情况
- 在不包含空位置的列中,有两列或者两列以上的和不相等的情况
- 空位置所在的行与列的和不相等的情况
最后记得求和要开long long 就可以了。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int a[600][600];
int l,r;
long long suml,sumr;
long long tmp;
long long sumx[600];
long long sumy[600];
long long tempx,tempy;
int check()
{
for(int i=1;i<=n;i++)
{
if(i==l) continue;
for(int j=1;j<=n;j++)
sumx[i]+=a[i][j];
tempx=sumx[i];
}
for(int i=1;i<=n;i++)
{
if(i==r) continue;
for(int j=1;j<=n;j++)
sumy[i]+=a[j][i];
tempy=sumy[i];
}
for(int i=1;i<=n;i++)
{
if(i==l) continue;
for(int j=1;j<=n;j++)
{
if(j==r) continue;
if(sumx[i]!=sumy[j])
return 0;
}
}
for(int i=1;i<=n;i++)
{
if(i==l) continue;
for(int j=i;j>=1;j--)
{
if(j==l) continue;
if(sumx[i]!=sumx[j])
return 0;
}
}
for(int i=1;i<=n;i++)
{
if(i==r) continue;
for(int j=i;j>=1;j--)
{
if(j==r) continue;
if(sumy[i]!=sumy[j])
return 0;
}
}
tmp=tempx-suml;
if(tmp<=0)return 0;
return 1;
}
int main()
{
scanf("%d",&n);
if(n==1)
{
printf("-1");
return 0;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
scanf("%d",&a[i][j]);
if(!a[i][j]) l=i,r=j;
}
for(int i=1;i<=n;i++)
suml+=a[l][i];
for(int i=1;i<=n;i++)
sumr+=a[i][r];
if(suml!=sumr)
{
printf("-1");
return 0;
}
if(!check())printf("-1");
else printf("%lld",tmp);
return 0;
}T2 新年出行
题目大意:
有一个图上有n个点,并且有n条单向的边。现在有任意的机会使得一条路的方向改变,求有多少种方法可以使得图中没有环。并将答案%1000000007
输入:
第一行一个正整数 N,表示 N 个点。 第二行,N 个由空格隔开的整数。如果第 i 个整数为 j,表示第 i 个点到第j个点有一条单向边。 注意:这 N 个数恰好是 1 到 N 的一个全排列。
输出:
让这 N 个点间的单向边不产生环的总方案数.
数据范围:
2<=N<=10^5
样例解释:
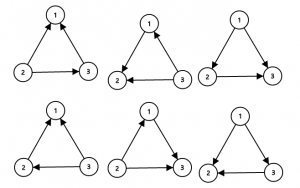
题目分析:
因为出度,入度都是1,不存在自边 ,所以这个图就是一个环或者是多个环
因为一个含有k条边的环可以改变的方案数是2k 除去顺时针环和逆时针环的情况 所以就是2k-2 种
最后将所有的环乘到一起就是答案 注意要开long long
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int n,sum,tmp;
int a[101000];
int path[101000];
bool book[101000];
void dfs(int x)
{
sum++,book[x]=true;
if(book[a[x]]) return ;
dfs(a[x]);
}
void work()
{
for(int i=1;i<=n;i++)
{
sum=0;
if(!book[i])
{
dfs(i);
path[++path[0]]=sum;
}
}
return ;
}
long long calc(int x)
{
long long tmp=1;
for(int i=1;i<=x;i++)
tmp=(tmp*2)%1000000007;
return tmp;
}
void check()
{
long long sum=1;
for(int i=1;i<=path[0];i++)
sum=(sum*(calc(path[i])-2))%1000000007;
printf("%lld",sum);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
work();
check();
return 0;
}T3 正月十五挂彩灯
题目分析:
这个DP方程还是比较易懂的。
设f[i][j][k]表示第i盏灯颜色为j且满意度为k时的最小维修开销。
三维数组 时间复杂度是O(nm^2k)
第i盏灯不需要维修:
f[i][color[i]][k]=min(f[i][color[i]][k],f[i-1][j][color[i]==j?k:k-1]);
第i盏灯需要维修:
f[i][j][k]=min(f[i][j][k],f[i-1][l][l==j?k:k-1]+cost[i][j]);
初始化:数组置为极大值,并且需要讨论第一盏灯的情况
第一盏灯不需要维修, f[1][color[1]][1]=0;
第一盏灯需要维修,f[1][k][1]=cost[1][k];
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,nmp;
int f[110][110][110];
int color[110];
int cost[110][110];
int main()
{
scanf("%d%d%d",&n,&m,&nmp);
for(int i=1;i<=n;i++)
scanf("%d",&color[i]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&cost[i][j]);
memset(f,0x7f,sizeof f);
if(color[1]>0) f[1][color[1]][1]=0;
else for(int i=1;i<=m;i++)
f[1][i][1]=cost[1][i];
for(int i=2;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(color[i]>0)
for(int k=1;k<=nmp;k++)
f[i][color[i]][k]=min(f[i][color[i]][k],f[i-1][j][(color[i]==j)?k:k-1]);
else
for(int k=1;k<=nmp;k++)
for(int l=1;l<=m;l++)
f[i][j][k]=min(f[i][j][k],f[i-1][l][(l==j)?k:k-1]+cost[i][j]);
}
}
int ans=0x7f7f7f7f;
for(int i=1;i<=m;i++)
ans=min(ans,f[n][i][nmp]);
if(ans==0x7f7f7f7f) ans=-1;
printf("%d",ans);
}
