Description
给出一棵树,要求你为树上的结点标上权值,权值可以是任意的正整数 唯一的限制条件是相临的两个结点不能标上相同的权值,要求一种方案,使得整棵树的总价值最小。
Input
先给出一个数字N,代表树上有N个点,N<=10000 下面N-1行,代表两个点相连
Output
最小的总权值
Sample Input
10
7 5
1 2
1 7
8 9
4 1
9 7
5 6
10 2
9 3
Sample Output
14
题目分析
首先 这题不能黑白染色
考虑这样的一张图
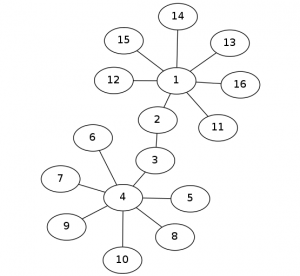
可以发现 这种情况下用3种颜色比用2种颜色更优
那么树形DP即可
表示以i为根的子树 i的颜色是j时候的最小总权值
第二维开到5就行QAQ
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
using namespace std;
int n;
int f[10010][10];
int head[10010],net[20010],to[20020];
int tot;
void add(int x,int y)
{
net[++tot]=head[x],head[x]=tot,to[tot]=y;
}
void dfs(int x,int temp)
{
for(int i=head[x];i;i=net[i])
{
if(to[i]==temp) continue;
dfs(to[i],x);
for(int j=1;j<=5;j++)
{
int tmp=0x3f3f3f3f;
for(int k=1;k<=5;k++)
{
if(j==k) continue;
tmp=min(tmp,f[to[i]][k]);
}
f[x][j]+=tmp;
}
}
for(int i=1;i<=5;i++) f[x][i]+=i;
}
int main()
{
scanf("%d",&n);
for(int x,y,i=1;i<n;i++)
scanf("%d%d",&x,&y),add(x,y),add(y,x);
dfs(1,0);
int ans=0x3f3f3f3f;
for(int i=1;i<=5;i++) ans=min(ans,f[1][i]);
printf("%d",ans);
return 0;
}
